The paper I read for this month brought up an interesting question I’ve always had but never really dug into: how do individual cells find things they can’t “see”? After all, there are lots of microbes out there who can’t always see where their next meal is coming from. How do they go about looking?
A group of scientists at Princeton University took a stab at the problem by studying the motion of individual slime mold amoeba (from the genus Dictyostelium) and published their findings in the (open access) journal PLoS ONE.
As one would imagine, if you have no idea where something is, your path to finding it will be somewhat random. What this paper sought to discover is what kind of random motion do amoeboid-like cells use? To those of you without the pleasure of training in biophysics or stochastic processes, that may sound like utter nonsense, but suffice to say physicists and mathematicians have created mathematically precise definitions for different kinds of “random motion”.
Now, if the idea of different kinds of randomness makes zero sense to you, then the following figure (from Figure 1 in the paper) might be able to help:
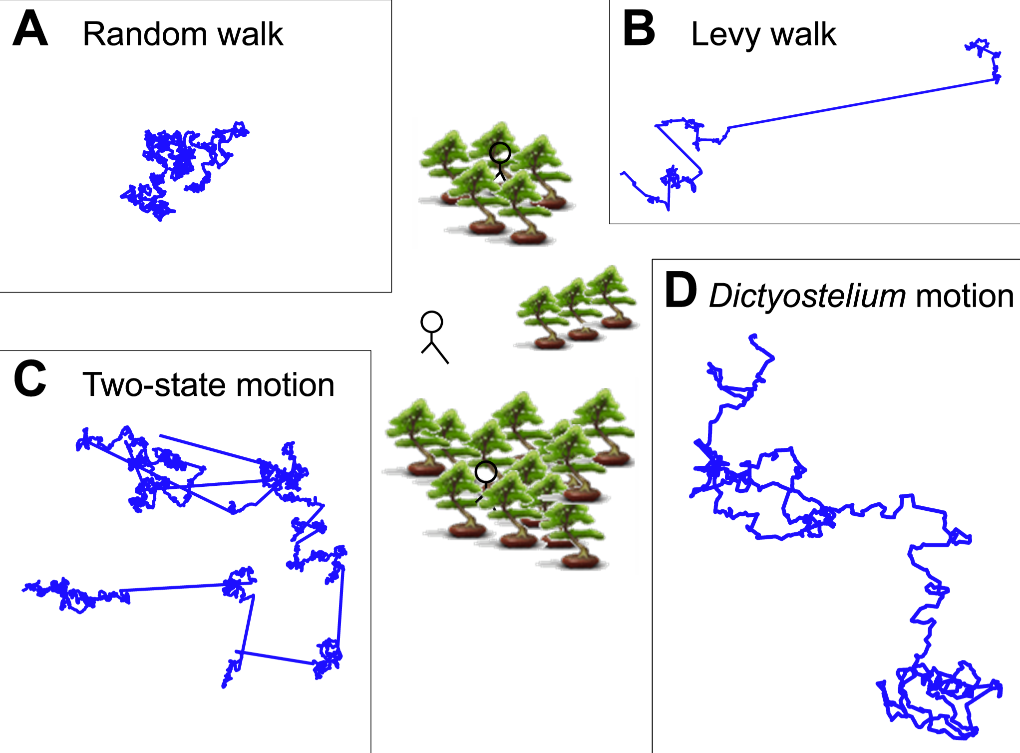
anel A describes a “traditional” random walk, where each “step” that a random walker takes is completely random (unpredictable and independent of the motion before it). As you can see, the path doesn’t really cover a lot of ground. After all, if you were randomly moving in different directions, you’re just as likely to move to the left as you are to move to the right. The result of this chaos is that you’re likely not to move very far at all (but likely to search a small area very thoroughly). As a result, this sort of randomness is probably not very useful for an amoeba hunting for food, unless for some reason it is counting on food to magically rain down on its lazy butt.
Panel B and C describe two other kinds of randomness which are better suited to covering more ground. Although the motion described in panel B (the “Levy walk”) looks very different from the “random walk” in Panel A, it is actually very similar on a mathematical/physical level. In fact, the only difference between the “Levy walk” and the “random walk” is that, in a “normal” random walk, the size of each step is constant, whereas the size of each “step” in a “Levy walk” can be different and, sometimes, extremely long. This lets the path taken cover a whole lot more ground.
A different way of using randomness to cover a lot of ground is shown in Panel C where, instead of taking big steps, the random path actually takes on two different types of motion. In one mode, the steps are exactly like the random walk in Panel A, where the path doesn’t go very far, but “searches” a local area very thoroughly. In another mode, the path bolts in a straight line for a significant distance before settling back into a random walk. This alternation between the different modes defines the “two-state motion” and is another way for randomness to cover more ground than a random walk.
And what do amoeba use? Panel D gives a glimpse of it. Unlike the nice theoretical paths from Panels A-C rooted around random walks and different size steps or different modes of motion, the researchers found that slime mold amoeba like to zig-zag around a general direction which seems to change randomly over the course of ~10 min. Panel A of Figure 2 (shown below) gives a look at three such random paths taken over 10 hours.
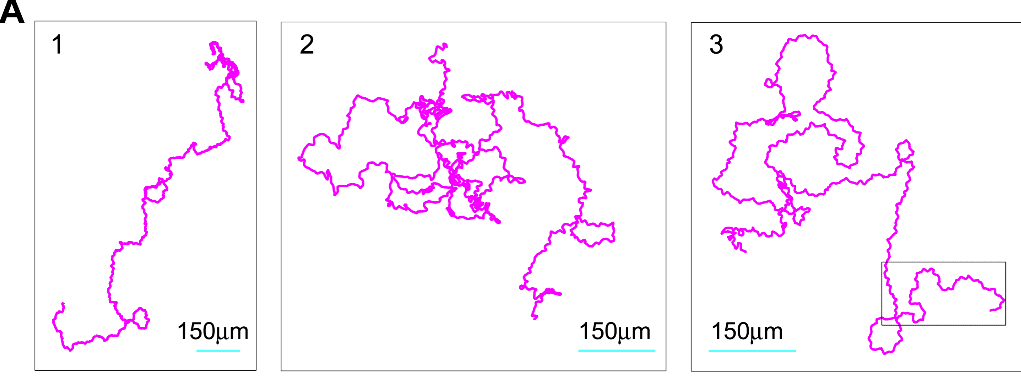
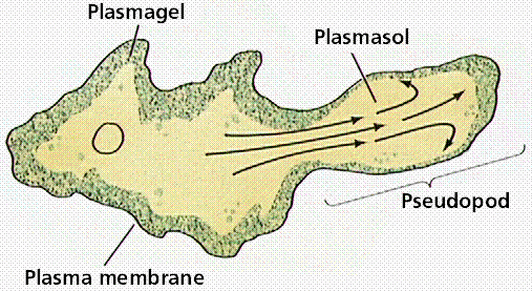
The reason for this zig-zagging, or at least the best hypothesis at the time of publication, is that, unlike theoretical particles, amoeba can’t just move in completely random directions with random “step” sizes. They move by “oozing” out pseudopods (picture below), and this physical reality of amoeba motion basically makes the type of motion the researchers discussed more likely and efficient for a cell trying to make its way through uncharted territory.
The majority of the paper actually covers a lot of the mathematical detail involved in understanding the precise nature of the randomness of amoeboid motion, and is, frankly, an overly-intimidating way to explain what I just described above. In all fairness, that extra detail is more useful and precise in terms of understanding how amoeba move and give a better sense of the underlying biochemistry and biophysics of why they move that way. But what I found most impressive was that the paper took a very basic and straightforward experiment (tracking the motion of single cells) and applied a rigorous mathematical and physical analysis of what they saw to understand the underlying properties.
The paper was from May 2008 and, according to the PLoS One website, there have been five papers which have cited it (which I have yet to read). But, I’d like to think that the next steps for the researchers involved would be to:
- See how much of this type of zig-zag motion applies to other cell types (i.e., white blood cells from our immune system), and why these differences might have emerged (different cell motion mechanisms? the need to have different types of random search strategies?)
- Better understand what controls how quickly these cells change direction (and understand if there are drugs that can be used to modulate how our white blood cells find/identify pathogens or how pathogens find food)
Paper: Li, Liang et al. “Persistent Cell Motion in the Absence of External Signals: a Search Strategy for Eukaryotic Cells.” PLoS ONE3 (5): e2093 (May 2008) – doi:10.1371/journal.pone.0002093

Leave a Reply